한빛출판네트워크

✅너비 우선 탐색

너비 우선 탐색^{BFS, Breadth-First Search}을 사용하면 두 항목 간 최단 경로를 찾을 수 있습니다. 그런데 이 최단 경로라 는 말은 여러 가지를 의미할 수 있습니다. 예를 들어, 다음과 같은 목적으로 너비 우선 탐색을 사용할 수 있습니다.

• 맞춤법 검사기(실제 단어에서 가장 적은 개수의 글자를 고쳐서 올바른 단어를 만드는 방법을 찾습니다)
• 주변에서 가장 가까운 의사 선생님 찾기
• 검색엔진 크롤러^crawler 제작하기

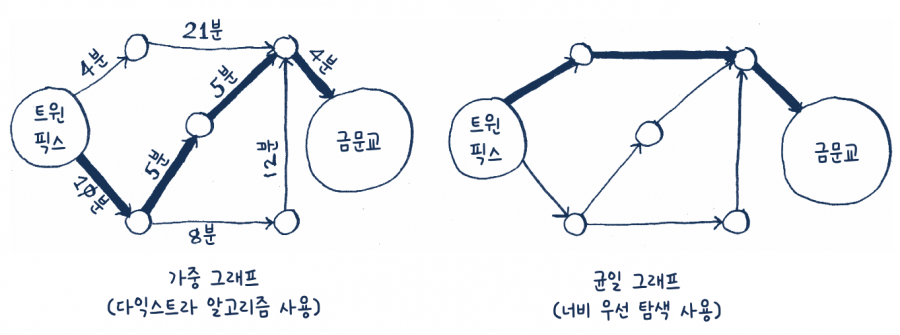
샌프란시스코에 있고, 트윈 픽스^{Twin Peaks}에서 금문교^{Golden Gate Bridge}까지 가고 싶다고 가정해 보세요. 버스로 가지만 최대한 적게 갈아타고 싶습니다. 선택할 수 있는 경로들은 다음과 같습니다.

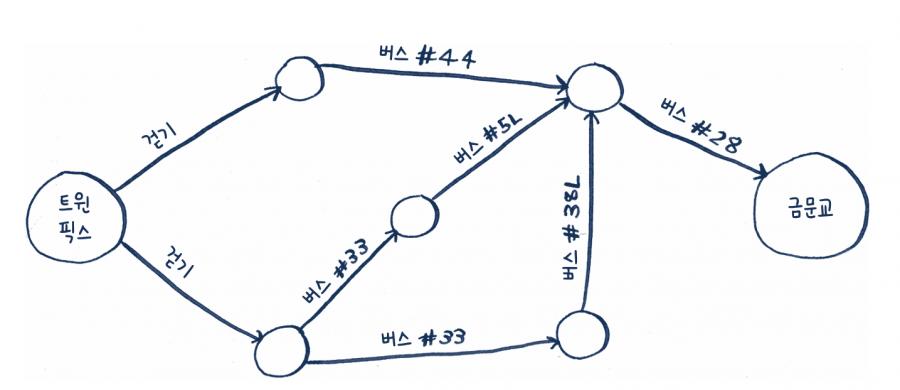
가장 적은 단계로 갈아타는 경로를 찾는 알고리즘은 무엇일까요? 우선 한 단계로 갈 수 있는 곳은 다음과 같이 그림에서 불이 켜진 곳입니다. 아직 금문교까지는 불이 켜지지 않았네요.

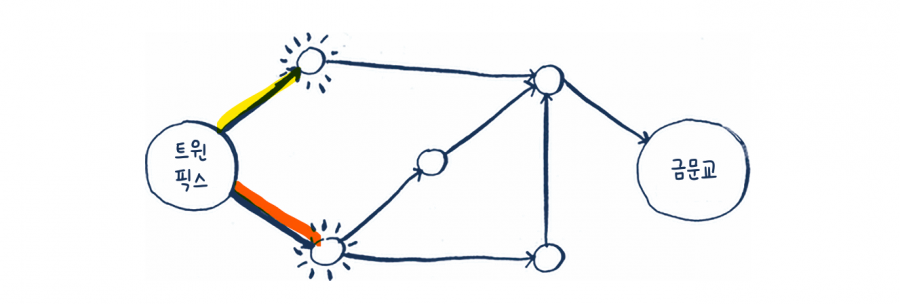
두 단계로 갈 수 있는 곳은 어디일까요? 아직도 금문교에는 불이 켜지지 않았습니다. 그러니까 두 단계로는 금문교에 도착할 수 없다는 거죠.

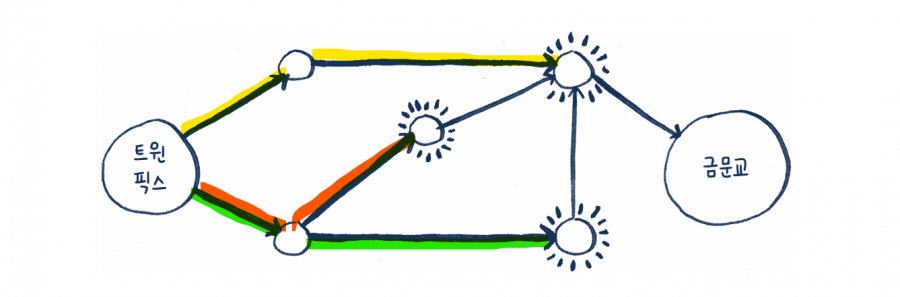
그럼 세 단계는 어떨까요? 아하! 이제 금문교에 불이 켜졌습니다.

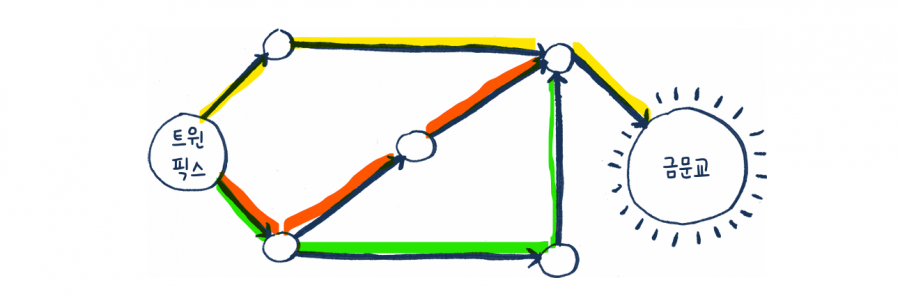
그러니까 이 경로로 트윈 픽스에서 금문교까지 가는 데 세 단계가 걸립니다.

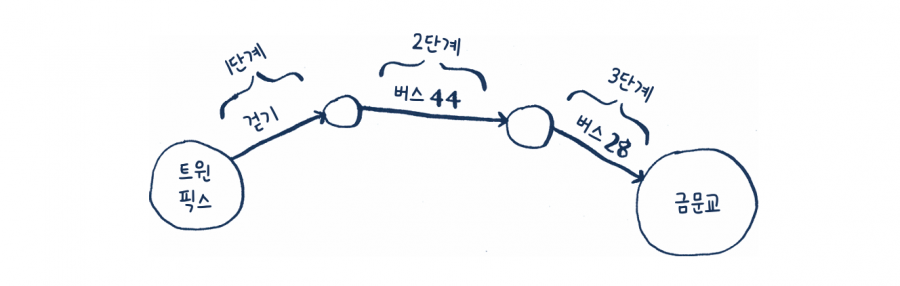
금문교로 갈 수 있는 다른 경로도 있지만, 4단계로 거리가 더 깁니다. 이 알고리즘을 통해 금문교까지의 최단 경로가 3단계라는 것을 알게 되었습니다. 이런 종류의 문제를 최단 경로 문제^{shortest-path problem}라고 합니다. 

최단 경로, 즉 가장 짧은 것을 찾아야 합니다. 목표는 우리가 친구 집까지 가는 최단 경로일 수도 있고, 웹 사이트를 탐색하는 것일 수도 있습니다. 우리가 웹 사이트를 볼 때도 네트워크는 우리의 컴퓨터에서 웹 사이트의 서버까지 최단 경로를 찾습니다. 이렇게 최단 경로 문제를 푸는 알고리즘을 너비 우선 탐색^{breadth-first search}이라고 합니다.

✅너비 우선 탐색 vs 다익스트라 알고리즘

방금 우리는 트윈픽스에서 금문교를 가는 경로를 구했습니다. 하지만 이 경로는 가장 빠른 길이 아니라 가장 짧은 길, 즉 최단 경로입니다. 왜냐하면 가장 적은 수의 구간^segment을 지나기 때문입니다. 하지만 각 구간을 지날 때마다 시간을 측정해 보면 더 빠른 경로가 있을 수도 있습니다.

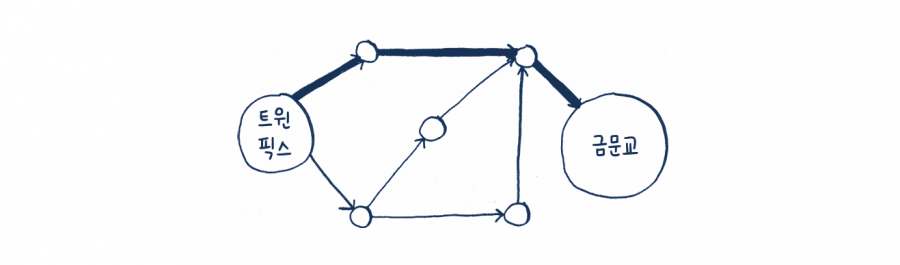
너비 우선 탐색 알고리즘은 가장 적은 수의 구간을 지나는 경로를 찾아냅니다. 만약 위의 가장 빠른 경로를 찾고 싶다면 어떻게 해야 할까요? 다익스트라 알고리즘^{Dijkstra’s algorithm}이라고 하는 다른 알고리즘을 사용하면 최단 시간 경로를 구할 수 있습니다.

✅다익스트라 알고리즘

다음 그래프에서 다익스트라 알고리즘이 어떻게 동작하는지 살펴보겠습니다.

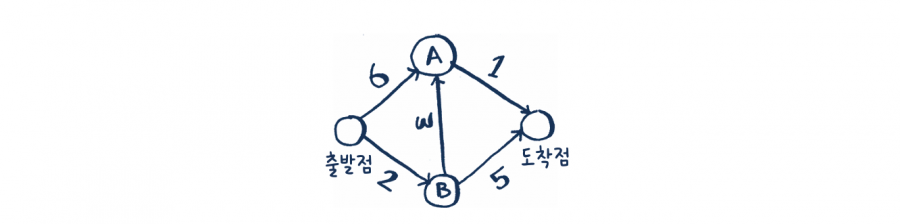
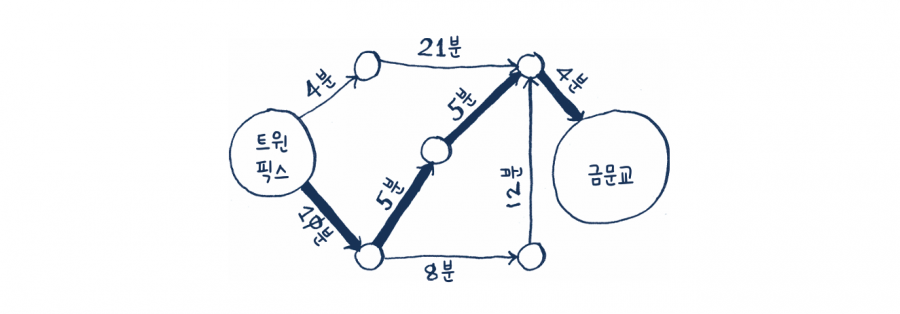
각 구간은 분 단위로 표시한 이동 시간이 소요됩니다. 다익스트라 알고리즘을 사용해서 출발점에서 도착점으로 가는 최단 시간 경로를 구해 보겠습니다. 만약 우리가 너비 우선 탐색을 사용한다면 다음처럼 최단 경로를 얻겠죠.

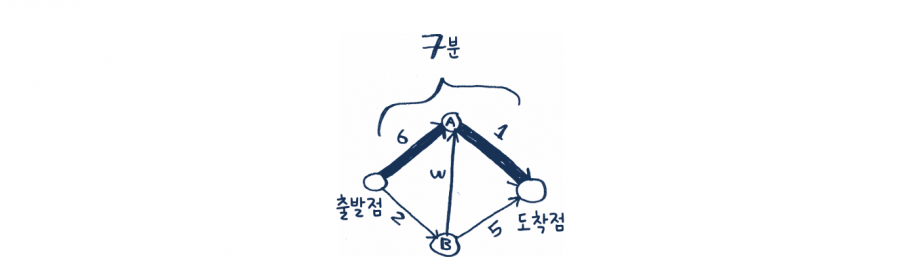
하지만 이 경로는 7분이 걸립니다. 더 빠른 경로를 찾을 수 있는지 살펴볼게요. 다익스트라 알고리즘은 4단계로 이루어집니다.

1. 가장 ‘가격이 싼’ 정점을 찾습니다. 가장 가격이 싼 정점이란 도달하는 데 시간이 가장 적게 걸리는 정점을 말합니다.
2. 이 정점의 이웃 정점들의 가격을 조사합니다. 이 말이 무슨 뜻인지는 곧 설명하겠습니다.
3. 그래프상 모든 정점에 대해 이러한 일을 반복합니다.
4. 최종 경로를 계산합니다.

• 1단계: 가장 싼 정점을 찾습니다. 우리는 지금 출발점에 있고 정점 A와 정점 B 중 어느 곳으로 가야 할지 고민하고 있습니다. 각 정점으로 가는 데 시간이 얼마나 걸리나요?

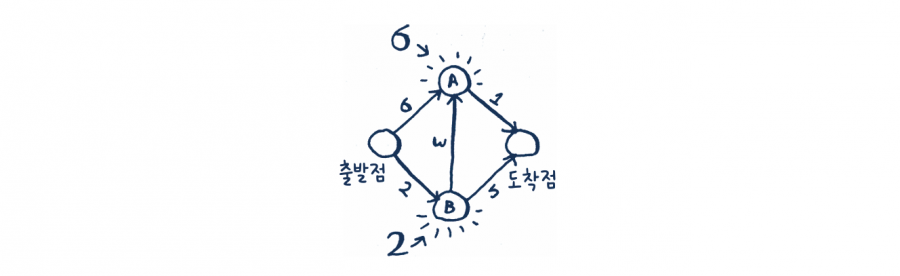
정점 A로 가는 데 6분이 걸리고, 정점 B로 가는 데 2분이 걸립니다. 나머지 정점에 대해서는 아직 알지 못합니다. 도착점까지 가는 데 얼마가 걸리는지는 아직 알 수 없기 때문에 일단 무한대라고 하겠습니다. 지금까지는 정점 B가 가장 가까우며 2분이 걸립니다.

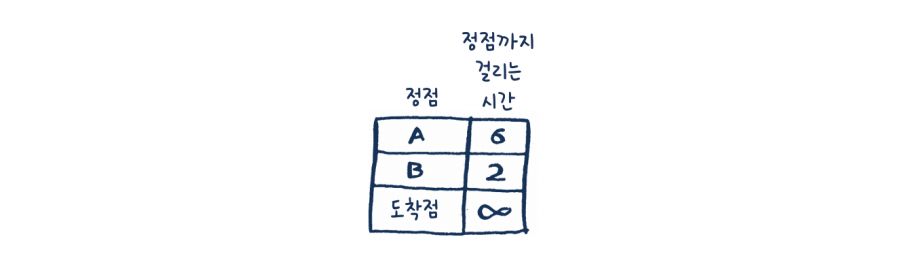
• 2단계: 정점 B의 모든 이웃 정점에 대해 정점 B를 통과하여 정점 A에 도달하는 데 걸리는 시간을 계산합니다.

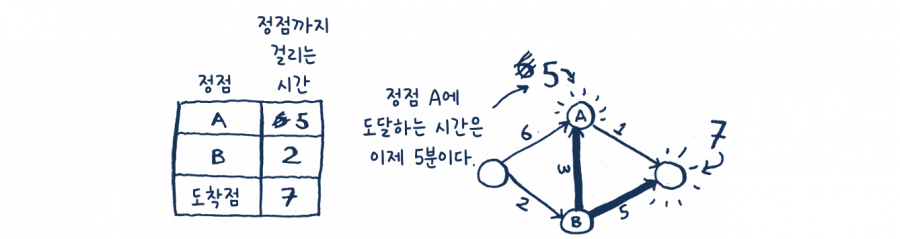
이제 우리는 정점 A에 도달하는 더 빠른 경로를 찾았습니다. 예전에는 정점 A에 도달하는 데 6분이 걸렸죠.

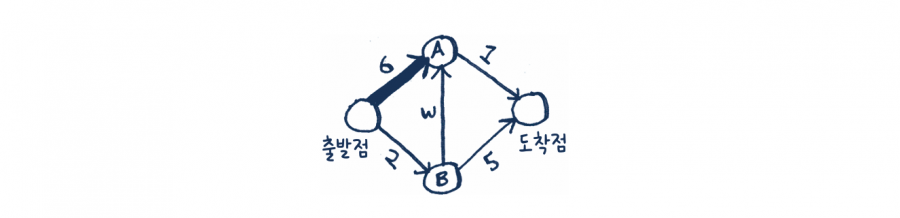
하지만 정점 B를 통해서 정점 A로 가면 5분밖에 걸리지 않습니다.

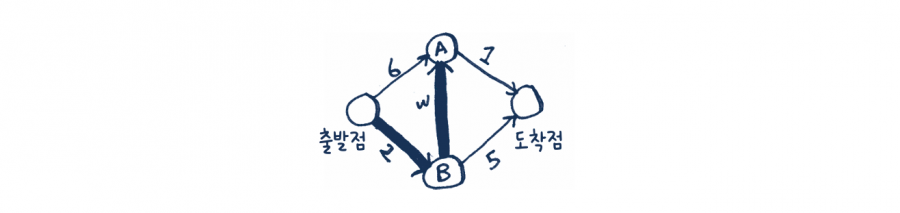
정점 B의 이웃 정점에 대해 더 빠른 경로를 찾으면 가격을 바꿉니다. 이 경우에는 다음과 같은 경로를 찾았습니다.

• 정점 A로 가는 더 짧은 거리(6분에서 5분으로 단축)
• 도착점까지 가는 더 짧은 거리(무한대에서 7분으로 단축)

• 3단계: 이제 지금까지 한 일을 반복합니다.

• 다시 1단계: 가장 빨리 도착할 수 있는 정점을 찾습니다. 정점 B는 이미 처리했고, 정점 A가 그다음으로 시간이 적게 걸립니다.

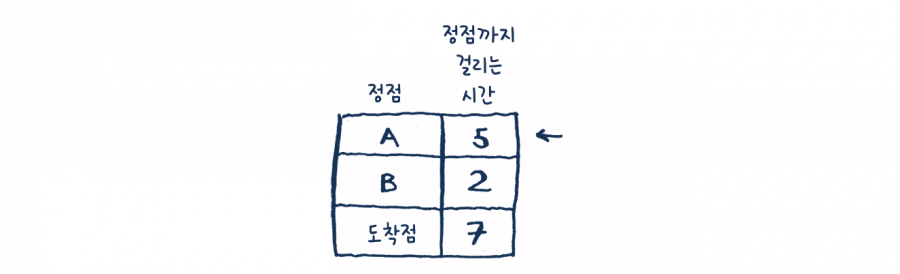
• 다시 2단계: 정점 A의 이웃 정점에 대한 가격을 수정합니다.

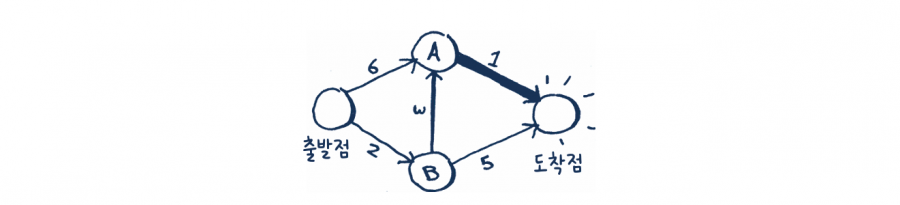
와! 이제 도착점까지 가는 데 걸리는 시간이 6분으로 줄었습니다! 이제 모든 정점에 대해 다익스트라 알고리즘을 돌려 보았습니다(도착점에 대해서는 돌릴 필요가 없습니다). 우리는 다음과 같은 사실을 알게 되었습니다.

• 정점 B에 도달하는 데는 2분이 걸립니다.
• 정점 A에 도달하는 데는 5분이 걸립니다.
• 도착점에 도달하는 데는 6분이 걸립니다.

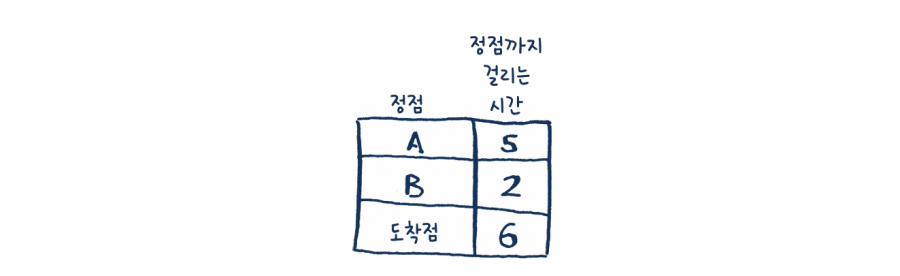
최종 경로는 다음과 같습니다.

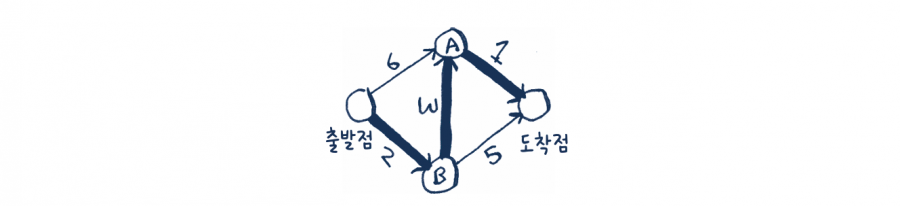
너비 우선 탐색으로는 이 경로를 찾지 못할 겁니다. 이 경로는 구간이 3개나 되고, 2개의 구간만으로 출발점에서 도착점으로 가는 경로도 존재하니까요.

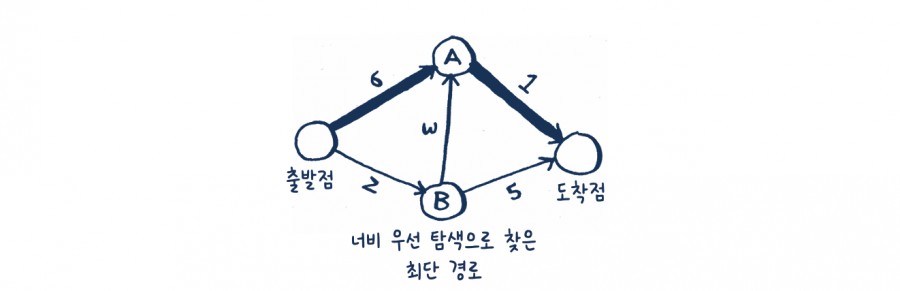
너비 우선 탐색은 두 정점 간 최단 경로를 찾는다고 했는데, 이때의 ‘최단 경로’란 가장 적은 수의 구간을 가지는 경로입니다. 하지만 다익스트라 알고리즘은 각 구간에 대해 숫자 혹은 가중치를 줄 수 있습니다. 그리고 전체 가중치의 합이 가장 작은 구간을 찾습니다.

정리하자면 다익스트라 알고리즘은 다음 4단계로 이루어집니다.

1. 가장 가격이 싼 정점, 즉 도달하는 데 시간이 가장 적게 걸리는 정점을 찾습니다.
2. 이 정점의 이웃 정점에 대해 현재 가격보다 더 싼 경로가 존재하는지 확인합니다. 만약 존재한다면 가격을 수정합니다.
3. 그래프의 모든 정점에 대해 이러한 일을 반복합니다.
4. 최종 경로를 계산합니다.

위 콘텐츠는 『그로킹 알고리즘(개정판)』의 내용을 재구성하여 작성되었습니다.
책에서 다익스트라 알고리즘이 동작하는 예시를 확인해 보세요.