IT/모바일
제공 : 한빛 네트워크
저자 : 존몽건, 노아 수오야넨 킨들러, 에릭 기게리
역자 : 서환수
출처 : 프로그래밍 면접, 이렇게 준비한다
실제 프로그래밍 인터뷰 문제들
 이제 나와 나의 친구들이 MS 인터뷰에서 받은 문제를 정리해보자. 그 중 몇 문제에 대해서는 내가 생각하는 답안을 정리해보았다. 하나 일러두고 싶은 것은 질문의 난이도는 면접을 보는 팀에 따라 꽤 차이가 난다는 것이다. 일반적으로 알고리즘 문제를 묻는 것은 큰 차이가 없지만, 팀의 성격에 따라 난이도가 다를 수 있다. 인턴 포지션 중 테스팅을 전문으로 하는 SDET이라는 포지션
은 자기가 짠 코드를 어떻게 디버깅 및 테스트할 것인가를 더 묻기도 한다.
이제 나와 나의 친구들이 MS 인터뷰에서 받은 문제를 정리해보자. 그 중 몇 문제에 대해서는 내가 생각하는 답안을 정리해보았다. 하나 일러두고 싶은 것은 질문의 난이도는 면접을 보는 팀에 따라 꽤 차이가 난다는 것이다. 일반적으로 알고리즘 문제를 묻는 것은 큰 차이가 없지만, 팀의 성격에 따라 난이도가 다를 수 있다. 인턴 포지션 중 테스팅을 전문으로 하는 SDET이라는 포지션
은 자기가 짠 코드를 어떻게 디버깅 및 테스트할 것인가를 더 묻기도 한다.
참고로 구글과 같은 기업도 난이도의 차이가 있을 뿐 큰 흐름은 같다고 보면 될 것이다. 하나 알아두어야 할 것은 모든 소프트웨어 업체들이 이런 식으로 면접을 보는 것은 아니라는 점이다. IBM의 어떤 부서 같은 경우에는 마이크로소프트와 구글의 알고리즘 면접 방식을 그다지 좋게 생각하지 않는 곳도 있기 때문이다. 이 책의 14장에서 다루고 있는 지식 기반의 문제를 던지는 곳도 많다는 것을 알아두길 바란다.
[인터뷰 문제]
C/C++로 프로그래밍을 해본 사람이라면 strcpy, memcpy, memmove와 같은 복사 함수를 사용해보았을 것이다. 그런데 예를 들어, 다음과 같은 memcpy 함수에서 dest와 src의 메모리 공간이 서로 겹친다면 어떻게 될까?
겹쳐지는 부분은 아래와 같이 두 가지 경우로 생각할 수 있을 것이다.
1)의 경우에는 src의 뒷부분과 dst의 앞부분이 겹친다. 이 경우에 src의 뒷부분은 결국 파괴될 것이다. 이 경우에는 뒷부분(높은 주소)부터 복사를 시작하면 될 것이다. 2)의 경우에는 반대로 낮은 주소부터 복사를 하면 될 것이다. 찬찬히 생각하면 어려운 문제는 아닐 것이다. 참고로 memmove의 소스는 아래와 같다. 이 소스는 Microsoft Visual Studio 2005가 설치하는 각종 파일 중 하나인 memcpy.asm 파일에서 발췌한 것이다.
[인터뷰 문제]
이 문제는 SDET로 면접을 본 친구에게 들은 문제이다.
“메모리 할당 함수인 malloc과 free를 만들었다고 하자. 어떻게 테스트할 것인가?”
일단 기본적인 메모리 할당이 제대로 되는지 살펴봐야 할 것이다. 할당한 메모리 블록들이 서로 겹치는 것이 없고 해제 시 문제없이 해제되는지 여러 가지 가능한 경우를 가지고 테스트를 해야 할 것이다. 여기까지는 누구나 생각할 수 있는 답변이고, 또 어떤 것을 테스트하면 좋을까?
먼저 성능을 따져봐야 할 것이다. 실제로 어떤 프로그램들은 malloc/free를 1초에 수백만 번 호출하는 경우도 있다. 이런 경우 이 함수들에서 병목 현상이 일어나는지 살펴봐야 할 것이다. 단순히 호출하는데 걸리는 시간뿐만 아니라, 이제는 듀얼코어가 기본인 환경이므로 멀티프로세서일 때의 성능도 언급하면 좋을 것이다. 실제로 일반적인 malloc/free의 구현은 멀티프로세서 환경에서 그다지 좋지가 않다.
특히 false sharing이라는 문제가 발생하여 많은 프로세서가 있는 환경에서는 speedup이 좋지 않게 나온다. (False sharing을 좁은 공간에서 설명하기는 쉽지 않다. 그래도 최대한 간략하게 설명하면, 보통 캐쉬 라인의 크기는 64 바이트와 같이 여러 개의 데이터가 들어갈 수 있다. 그리고 여러 프로세서가 이 캐쉬 라인을 공유하면 이 단위로 공유가 된다. 그래서 같은 캐쉬 라인에 4바이트짜리 데이터가 두 개 있고 이 데이터가 각각 다른 CPU로부터 사용이 된다면, 불필요하게 이 캐쉬 라인을 invalidate시키는 문제가 발생한다(이 부분을 제대로 이해하려면 cache coherence protocol 중 대표적인 MESI 프로토콜을 알아야 한다). 생각보다 이 문제는 성능에 심각한 영향을 미친다.) 따라서 이러한 것도 고려하면 어떨까라는 답변을 하면 멋질 것이다. (멀티프로세서 환경을 고려한 대표적인 메모리 관리자로 Hoard memory allocator가 있다. http://www.hoard.org/를 방문해보라.)
[인터뷰 문제]
 이번에는 convex hull에 관한 문제이다. 그래픽스 수업을 듣지 않은 사람이라면 convex hull 자체에 대해서도 생소할 것이다. convex hull은 수학적인 의미도 있지만 좀 더 직관적으로 그림으
로 설명하면 주어진 점들을 감싸는 최소한의 공간을 뜻한다. 2차원 같은 경우는 아래 그림과 같다. (http://en.wikipedia.org/wiki/Convex_hull)
이번에는 convex hull에 관한 문제이다. 그래픽스 수업을 듣지 않은 사람이라면 convex hull 자체에 대해서도 생소할 것이다. convex hull은 수학적인 의미도 있지만 좀 더 직관적으로 그림으
로 설명하면 주어진 점들을 감싸는 최소한의 공간을 뜻한다. 2차원 같은 경우는 아래 그림과 같다. (http://en.wikipedia.org/wiki/Convex_hull)
그림에서 보다시피 오목한 부분 (concave)가 없고 볼록한 부분(convex)만 있다. 그렇다면 이 convex hull을 어떻게 하면 구할 수 있을까?
이 문제는 이미 오랫동안 연구된 것이고 좋은 time complexity를 가지는 알고리즘도 많이 발견되었다. 그러나 실제 면접 볼 때 이런 천재적인 알고리즘을 요구하는 것은 아니다. 가장 간단한 알고리즘부터 차근차근 만들고 좀 더 개선할 여지가 있는지를 생각해서 말하면 좋을 것이다. 여기서는 가장 간단한 방법만 하나 소개할 예정이다. 그리고 좀 더 자세한 내용은 흔히 CLRS 책으 로 불리는 유명한 알고리즘 책인『 Introduction to Algorithms』(B y Cormen, Thomas H., Leiserson, Charles E., Rivest, Ronald L., Stein, Clifford, MIT Press)를 참고하기 바란다.
가장 간단한 방법 중 하나로 “Jarvis’s march(혹은 Gift wrapping)” 알고리즘이 있다. 말 그대로 감싸듯이 convex hull을 찾는 알고리즘이다. 아래 그림은 이 알고리즘이 어떻게 작동하는지 간단하게 보여주고 있다. (http://en.wikipedia.org/wiki/Gift_wrapping_algorithm)
먼저 가장 왼쪽에 있는 점인 P0를 찾는다. 그리고 다음 점 P1은 P0와 이루는 각이 가장 작은 녀석을 고르면 된다. 이 과정을 반복하면 convex hull을 찾을 수 있다. 앞서 소개한 CLRS 책에는 이와 다른 방법으로 알고리즘을 설명하고 있다. 다소 다르기는 하지만 전체적인 맥락은 차이가 없다. 다만 지금 그림에서 소개한 방법은 마지막으로 선택된 점의 각을 기억해야 한다. 그리고 하나 생각해볼 것은 가장 작은 각도를 만드는 점이 하나가 아니라 여러 개일 때 이것을 어떻게 해결할 것인가도 생각해보면 좋을 것이다. 이런 경우 영어로는 ~ breaks tie by selecting the furthest point ~와 같이 표현하면 된다.
이 알고리즘의 시간 복잡도를 계산해보자. 전체 점들의 개수를 n개라고 할 때, 다음 점을 찾는 과정은 각도를 구한 뒤 가장 작은 녀석을 찾으면 되므로 O(n)만큼의 시간이 걸릴 것이다. 그리고 이 과정을 convex hull에 포함될 점들의 개수 h만큼 수행하게 될 것이다. 따라서 알고리즘의 수행 시간은 O(nh) 꼴이 된다. 그래서 최악의 경우에는 h가 n과 같을 수가 있으므로 그 때는 O(n2) 알고리즘을 얻게 된다. 반면 h가 logn과 비슷하다면 이 방법은 상당히 우수한 성능을 보일 것이다. 그러나 알고리즘이 이렇게 미리 예측할 수 없는 h에 의존적이므로 항상 좋은 성능을 주는 것은 아니다. 반면 Graham’s Scan 방식은 O(nlogn)이라는 시간을 준다.
[인터뷰 문제]
주어진 두 정수를 나누는 함수를 만드는 문제이다. 물론 나눗셈 연산자(/)는 사용할 수 없다.
알고리즘은 간단하게 루프를 돌면서 a에서 b를 계속 빼면 몫을 구할 수 있다. 여기까지는 간단하나 여러 예외 사항을 잘 고려해야 한다. 일단 0으로 나눠지는 경우는 손쉽게 검사를 할 수 있다. 또한 주어진 수가 음수라면 절대값으로 만든 뒤에 계산을 하는 것이 편할 것이다. 그런데 단순히 절대값을 만들기 위해 -1을 곱하는 것은 문제가 발생할 수 있다. 보통 정수 표현은 2의 보수법(2’scomplement)으로 표현을 하는데, 음수의 범위가 양수보다 하나 더 크다. 예를 들어, 8비트라면 -128부터 127까지 표현이 가능하다. 따라서 -128에 단순히 -1을 곱하면 잘못된 값을 얻을 수 있다. 이 부분 역시 적절히 고려를 해야 할 것이다.
[인터뷰 문제]
문제는 간단하다. 예를 들어, {1, 7, 4, 9}라는 배열과 13이라는 숫자가 주어지면 4+9가 13을 만족하므로 답은 true가 될 것이다. 반면에 20이라는 숫자가 주어지면 만족하는 쌍이 없으므로 false를 반환하다. 혹은 하나 이상의 조합이 나올 수도 있는데, 이런 경우에는 어떤 것을 먼저 보여줘도 무방하다(이런 이야기를 해주지 않았으면 자기가 찾아서 이런 경우는 어떻게 하면 좋은지 직접 이야기를 하는 것이 좋다. 항상 면접 보는 사람과 많은 이야기를 하는 것이 중요하다).
가장 간단하게는 O(n2) 알고리즘으로 모든 쌍에 대해서 검사를 하는 것이다. 물론 이런 알고리즘을 요구하지 않는다. 이제 좀 더 좋은 성능을 위해 O(n) 만큼의 공간을 이용하는 방법을 생각해보자. 만약 hash table 자료 구조를 이용할 수 있다면 O(n) 시간에 답을 쉽게 구할 수 있다. hash table에 자료를 넣거나 검색하는 것은 상수 시간에 완료되기 때문이다. 그렇게 어렵지 않으므로 여기에 코드는 적지 않는다.
그러면 공간을 더 활용하지 않고 좀 더 똑똑히 할 수 있는 방법은 없을까? 만약 주어진 배열이 오름차순으로 정렬이 되어있다면? 이런 경우 공간은 더 사용하지 않으면서 O(n) 시간에 답을 구할 수 있는 방법이 있다.
먼저, 가장 작은 원소인 첫 번째 원소를 가리키는 왼쪽 인덱스 변수와 가장 큰 원소인 마지막 원소를 가리키는 오른쪽 인덱스 변수를 두자. 그리고 이 둘의 합을 구한 뒤 주어진 수와 크기를 비교하자. 만약 합이 주어진 수보다 작다면 왼쪽 인덱스를 증가시키고, 크다면 오른쪽 인덱스를 감소시킨다. 그리고 계속 반복을 하면서 같아지는지 확인을 하자. 루프는 최대 배열 원소의 개수만큼 반복하기 때문에 O(n) 시간에 완료된다. 코드는 아래와 같다.
참고로 이 문제를 푸는 데 도움을 주신 iwongu, 시즈하, 에이쥬어, 그리고 silverbird님께 감사의 말씀을 전한다. 지금 생각하면 어렵지 않은 문제이다. 아니 쉬운 문제이다. 그런데 3시간 동안의 면접으로 지친 가운데 이런 문제를 또 받으면 머리가 아파서 더 생각하기가 귀찮을 정도였다. 사실 나는 hash table까지 이용하는 답이면 충분하다고 생각했는데, 난데 없이 추가 공간 없이 O(n)에 작동하는 걸 생각해보라는 질문을 듣고 당황하였다. 역시 면접 보기 전날 충분한 숙면과 컨디션 유지는 필요 조건임을 다시 깨달았다.
[인터뷰 문제]
n개의 비트로 이루어진 2진수에서 연속된 1이 나타나지 않는 경우는 몇 개나 있을까?
이 문제는 코딩 문제라기 보다는 퀴즈에 가까운 문제라고 볼 수 있다. 그러나 이 문제는 결코 간단하지 않는 귀납적 사고 능력을 요구하고 있다. 이런 귀납적 사고 능력은 실제 프로그래밍에서도(예를 들어, dynamic programming) 아주 유용하게 사용할 수 있는 것이므로 이러한 능력을 기르는 것은 매우 중요하다. 보통 이런 내용은 전산학과 과목 중 이산 수학에서 다룬다. 그리고 12장의 내용과도 어느 정도 방향을 같이 하는 것이라고 보면 될 것이다. 실제로 이런 문제를 인터뷰에서 묻는 경우도 있었다.
예를 가지고 문제를 다시 설명해보자. 2비트라면 총 가능한 경우의 수는 00, 01, 10, 11로서 4가지이다. 여기서 1이 연속으로 나타나지 않는 경우는 00, 01, 10 총 3가지이다. 이렇게 n개의 0과 1로 이루어진 수열에서 연속된 1이 없는 경우의 수(이것을 C(n)으로 표현하자)를 찾는 것이 이 문제가 요구하는 답이다. 이런 문제의 시작은 일단 손으로 낙서를 해가며 규칙을 찾아야 한다. C(3)까지 한 번 직접 구해보자.
이런 순열의 경우 일반항을 구하기 위해서는 점화식을 찾는 것이 첫번째로 할 일이다. 점화식은 영어로 recurrence로 표현이 되며, 각종 재귀 알고리즘의 시간 복잡도를 기술하는 데도 많이 사용된다. 예를 들어, merge sort의 경우 T(n) = 2T(n/2) + O(n)으로 표현되고 Master"s theorem을 통해 O(nlogn)을 얻을 수 있다(자세한 것은 이산수학 책과 알고리즘 책을 참고하기 바란다).
점화식을 찾기 위해 수학 시간에 배운 수학적 귀납법을 이용해보자. C(n)의 해를 가지고 있다고 가정하자. 그리고 이제 C(n+1)을 기존의 해인 C(n)로 표현해보자.
숫자가 하나 더 늘었다는 소리는 n개의 순열 앞에 0 또는 1을 더 붙이는 것과 같다. 먼저 0이 추가되는 경우를 생각해보자. 생각하기 쉽게 이미 구한 C(3)을 가지고 생각하자. 이미 구한 5개의 답에 0을 앞에다 붙여도 여전히 이들은 주어진 조건을 만족하며 답으로 남는다. 즉, C(3)의 해를 고스란히 가져올 수 있다. C(4)에는 {0000, 0001, 0010, 0100, 0101}이 해로 포함이 될 것이다.
이제 1이 추가되는 경우를 생각해보자. 마찬가지로 C(3)의 해에다가 1을 더해보자. 앞의 3가지인 000, 001, 010은 문제 없다. 그러나 마지막 두 개는 1이 앞에 올 경우 1100처럼 되기 때문에 조건에 위배된다. 여기서 약간의 눈썰미를 동원해보자. 1을 더해도 조건을 만족하는 수들은 1000, 1001, 1010의 3가지이다. 그런데 이들은 처음 시작이 10으로 시작함을 알 수 있다. 그리고 그 뒤에 붙는 00, 01, 10은 C(2)의 해와 정확히 일치함을 발견할 수 있다. 즉, C(2)의 해에다가 10을 덧붙이는 것도 C(4)의 해가 된다.
따라서 C(4)는 결국 C(3)에다 0을 덧붙인 경우와 C(2)와 01을 덧붙인 경우로 생각할 수 있다. 즉, C(n)은 C(n-1) + C(n-2)가 되는 것이다. 그리고 이것은 바로 피보나치 수열과 정확하게 일치한다. 따라서 최종 정답은 아래와 같다.
먼저 문제 중 겹치는 부분이 있는가를 찾아야 한다. 풀이에서도 이미 보았듯이 C(n+1)의 해에는 C(n)의 해가 겹쳐있다. 이 관계를 잘 분석해서 점화식으로 표현을 한다. 그리고 bottom-up으로 값들을 차례대로 계산하면 원하는 답을 얻을 수 있다. 대표적으로 matrix-chain multiplication, longest common subsequence와 같은 문제가 있다. 단순히 리스트, 트리와 같은 자료 구조에 관련된 공부뿐만 아니라 동적 프로그래밍 혹은 greedy algorithm과 같이 알고 리즘 방법론도 숙지해야 할 것이다. 앞의 convex hull 문제에서 소개한 CLRS 책에는 이런 방법론들이 아주 자세히 설명되어 있다.
자, 그러면 응용 문제를 하나 더 풀어보자. 주어진 문제는 “연속된 1이 나타나지 않는 경우의 수”였다. 그러면 이 반대인 “연속된 1이 나타나는 경우의 수”는 어떻게 될까? D(n)을 구하고자 하는 수라고 표현하면 다음과 같을 것이다:
[인터뷰 문제]
어떤 숫자가 2의 거듭제곱수 (2, 4, 8, 16, 32, 64 , ...)인지 아닌지를 판단하는 코드를 작성하시오.
지금 소개한 문제는 정식 인터뷰에서 받은 문제가 아니라 Job Fair 같은 곳에서 이루어진 일종의 쪽지 시험에서 나온 문제였다. 앞에서도 이미 아마존 같은 기업은 이력서를 받는 그 자리에서 C 키워드 중 volatile이 무엇을 하는지 묻기도 한다고 쓴 바가 있다. 이 문제는 실제 Job Fair에서 어떤 기업이 이력서를 받으면서 학생들에게 준 간단한 코딩 테스트이다 그러나 결코 만만치 않은 문제일 수 있다.
만약 숫자들이 컴퓨터로 어떻게 표현이 되는지에 대한 정보가 없다면 다소 까다롭고 복잡한 루틴이 나올 수 있다(예를 들어, 2로 나눈 뒤에 나머지가 있는지 확인하고, 이 과정을 몫이 1이 될 때까지 반복하면 될 것이다). 그러나 거의 모든 컴퓨터들은 정수 표현을 2의 보수로 하기 때문에 이 특징을 활용하면 훨씬 빨리 문제를 풀 수 있다. 따라서 이 문제를 풀기 전, 문제에서 주어진 숫자들은 부호와 2의 보수로 주어졌다고 가정을 해보자. 항상 문제를 풀 때 부족하다고 느껴지는 가정은 쓰는 것이 좋다. 그리고 이 가정을 세우는 것도 중요한 능력 중에 하나이다.
먼저 2의 거듭제곱수들을 2진수로 표현을 해보자. 금방 규칙 하나를 발견할 수 있을 것이다. 오직 한 자리수만 1로 되어있고 나머지는 모두 0임을 확인할 수 있다. 단순하게는 32 혹은 64번만큼 루프를 돌면서 1이 하나만 켜져 있는지 보면 될 것이다. 아니면 대부분의 CPU가 지원하는 기본 명령인 BitScanForward와 BitScanReverse를 이용하는 방법도 있을 것이다. 14 LSB에서 시작하여 MSB로 가면서 1이 발견되면 그 위치를 알려주는 함수들이다(Reverse는 MSB에서 LSB로 탐색). 그래서 이 두 함수로부터 얻은 위치가 같으면 2의 거듭제곱수라고 판단할 수 있다. 그러나 이렇게 해도 뭔가 깔끔하고 아름답지가 못하다. 더 좋은 방법이 있다.
주어진 숫자에서 1을 한 번 빼보자. 그러면 2진수 표현 방법으로는 가장 먼저 발견된 1 뒤의 모든 숫자들이 모두 1로 변할 것이다. 그리고 원래 수와 AND연산을 한다면? 2의 거듭제곱수라면 결국 0이 얻어질 것이다. 이것이 가장 빠른 2의 거듭제곱수 판단 방법이다. 예를 들면 다음과 같다. x는 2의 거듭제곱수이고, y는 그렇지 않은 수이다.

이 정도면 충분히 이 원리에 대해서 이해가 갔으리라 믿는다. 그러나 여기서도 또 예외가 하나 있다. Boundary check를 해야 하는데, 0이 주어진다면 이 테스트로는 참이 얻어질 것이다. 또, 음수도 무시해야 할 것이다. 따라서 최종 정답은 (x > 0) && ((x & (x - 1)) == 0) 이 될 것이다. 좀 더 엄밀하게 말해 이 조건은 부호와 2의 보수로 표현된 정수 x가 2의 거듭제곱수인가와 필요충분조건을 이룬다.
[인터뷰 문제]
다음 매크로가 하는 일이 무엇인지 기술하시오.
많은 프로그래밍 경험이 있다면 이 매크로가 무엇을 하는 것인지 금방 알아차릴 것이지만, 그렇지 않다면 당혹스러울 수 있다. NULL을 이상하게 캐스팅을 하고 거기에 멤버 변수까지 접근하니 “이거 버그 아니야?”라고 갸우뚱할 수 있다. 그러나 이것은 올바른 코드이고 자주 사용되는 매크로이다.
이것은 주어진 class 혹은 struct에서 특정 멤버 변수의 offset을 알아내는 것이다. 컴파일러마다 혹은 컴파일러 옵션마다 struct 자료 구조에서 멤버 변수들의 공간을 할당할 때, alignment가 다를 수가 있다. 그래서 클래스에서 어떤 멤버 변수가 얼마나 떨어져 있는가를 알고 싶다면 이 매크로를 사용하여 유용하게 알 수 있다. 이 매크로의 경우에 a에는 클래스에 대한 포인터, b에는 멤버 변수 이름을 넘겨주면 이 변수의 오프셋을 알 수 있다. 0번 주소라는 잘못된 주소를 강제로 주어진 클래스 포인터 타입으로 바꾼 뒤에 멤버 변수의 주소를 반환하는 것이다.
예제 코드를 통해 이 매크로가 어떻게 작동하는지 살펴보자.
이런 매크로를 이용한 장난은 상당히 다양한데, 그래도 C/C++을 자신있게 다룬다고 말을 할 수 있다면 간단한 매크로 구문은 충분히 숙지해야 할 것이다.대표적으로 #define에서 사용되는 #와 ## preprocessor operator들이 있다. #는 stringizing operator라고 불리며 주어진 내용을 따옴표로 감싸 문자열로 바꿔주는 역할을 한다. ##는 Token-Pasting 혹은 merging operator라고 불 리며 앞 토큰과 뒤에 있는 토큰15을 이어주는 역할을 한다. 좀 더 자세한 예는 검색을 통해서 쉽게 찾을 수 있을 것이다.
지금까지 8문제를 풀어보았다. 보다시피 그 자리에서 아주 높은 수준의 번뜩이는 천재성을 요구하는 문제는 없다. 모두 기본적인 전산 실력이 있으면 풀수 있는 내용들이다.
마지막으로 이 문제들 외에 실제 면접에서 받은 문제 몇 개를 간략하게 소개하면 다음과 같다.
[정답]
저자 : 존몽건, 노아 수오야넨 킨들러, 에릭 기게리
역자 : 서환수
출처 : 프로그래밍 면접, 이렇게 준비한다
실제 프로그래밍 인터뷰 문제들
 이제 나와 나의 친구들이 MS 인터뷰에서 받은 문제를 정리해보자. 그 중 몇 문제에 대해서는 내가 생각하는 답안을 정리해보았다. 하나 일러두고 싶은 것은 질문의 난이도는 면접을 보는 팀에 따라 꽤 차이가 난다는 것이다. 일반적으로 알고리즘 문제를 묻는 것은 큰 차이가 없지만, 팀의 성격에 따라 난이도가 다를 수 있다. 인턴 포지션 중 테스팅을 전문으로 하는 SDET이라는 포지션
은 자기가 짠 코드를 어떻게 디버깅 및 테스트할 것인가를 더 묻기도 한다.
이제 나와 나의 친구들이 MS 인터뷰에서 받은 문제를 정리해보자. 그 중 몇 문제에 대해서는 내가 생각하는 답안을 정리해보았다. 하나 일러두고 싶은 것은 질문의 난이도는 면접을 보는 팀에 따라 꽤 차이가 난다는 것이다. 일반적으로 알고리즘 문제를 묻는 것은 큰 차이가 없지만, 팀의 성격에 따라 난이도가 다를 수 있다. 인턴 포지션 중 테스팅을 전문으로 하는 SDET이라는 포지션
은 자기가 짠 코드를 어떻게 디버깅 및 테스트할 것인가를 더 묻기도 한다.
참고로 구글과 같은 기업도 난이도의 차이가 있을 뿐 큰 흐름은 같다고 보면 될 것이다. 하나 알아두어야 할 것은 모든 소프트웨어 업체들이 이런 식으로 면접을 보는 것은 아니라는 점이다. IBM의 어떤 부서 같은 경우에는 마이크로소프트와 구글의 알고리즘 면접 방식을 그다지 좋게 생각하지 않는 곳도 있기 때문이다. 이 책의 14장에서 다루고 있는 지식 기반의 문제를 던지는 곳도 많다는 것을 알아두길 바란다.
[인터뷰 문제]
C/C++로 프로그래밍을 해본 사람이라면 strcpy, memcpy, memmove와 같은 복사 함수를 사용해보았을 것이다. 그런데 예를 들어, 다음과 같은 memcpy 함수에서 dest와 src의 메모리 공간이 서로 겹친다면 어떻게 될까?
void *memcpy(void* dest, const void* src, size_t count );실제로 C언어 표준 규약인 C99에서는 memcpy의 경우 두 메모리 공간이 겹쳐지는 것에 대해서는 정의를 하지 않고 있다. 즉, 어떤 일이 벌어질지 모르므로 항상 겹치지 않는 공간을 줘야만 한다(그래서 C99에는 “restrict”라는 qualifier가 양쪽 모두 붙어있다). 반면 memmove는 이런 겹치는 부분이 있을 때 알아서 잘 처리한다. 물론 이것을 처리하기 위한 비용은 더 들어갈 것이다. 그렇다면 memcpy도 겹치는 부분이 있다면 어떻게 처리하면 좋을까?
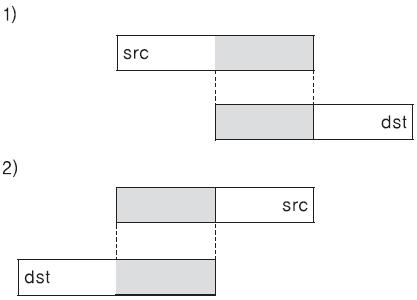
겹쳐지는 부분은 아래와 같이 두 가지 경우로 생각할 수 있을 것이다.

1)의 경우에는 src의 뒷부분과 dst의 앞부분이 겹친다. 이 경우에 src의 뒷부분은 결국 파괴될 것이다. 이 경우에는 뒷부분(높은 주소)부터 복사를 시작하면 될 것이다. 2)의 경우에는 반대로 낮은 주소부터 복사를 하면 될 것이다. 찬찬히 생각하면 어려운 문제는 아닐 것이다. 참고로 memmove의 소스는 아래와 같다. 이 소스는 Microsoft Visual Studio 2005가 설치하는 각종 파일 중 하나인 memcpy.asm 파일에서 발췌한 것이다.
void * memmove(void * dst, void * src, size_t count)
{
void * ret = dst;
if (dst <= src || dst >= (src + count)) {
/*
* Non-Overlapping Buffers
* copy from lower addresses to higher addresses
*/
while (count--)
*dst++ = *src++;
}
else {
/*
* Overlapping Buffers
* copy from higher addresses to lower addresses
*/
dst += count - 1;
src += count - 1;
while (count--)
*dst-- = *src--;
}
return(ret);
}
그리고 여기에서 부가적으로 생각해볼 수 있는 문제는 작성한 코드가 Endianness(Little-endian/Big-endian)에 영향이 있는지, Alignment에는 영향이 있는지 정도가 있을 것이다.
[인터뷰 문제]
이 문제는 SDET로 면접을 본 친구에게 들은 문제이다.
“메모리 할당 함수인 malloc과 free를 만들었다고 하자. 어떻게 테스트할 것인가?”
일단 기본적인 메모리 할당이 제대로 되는지 살펴봐야 할 것이다. 할당한 메모리 블록들이 서로 겹치는 것이 없고 해제 시 문제없이 해제되는지 여러 가지 가능한 경우를 가지고 테스트를 해야 할 것이다. 여기까지는 누구나 생각할 수 있는 답변이고, 또 어떤 것을 테스트하면 좋을까?
먼저 성능을 따져봐야 할 것이다. 실제로 어떤 프로그램들은 malloc/free를 1초에 수백만 번 호출하는 경우도 있다. 이런 경우 이 함수들에서 병목 현상이 일어나는지 살펴봐야 할 것이다. 단순히 호출하는데 걸리는 시간뿐만 아니라, 이제는 듀얼코어가 기본인 환경이므로 멀티프로세서일 때의 성능도 언급하면 좋을 것이다. 실제로 일반적인 malloc/free의 구현은 멀티프로세서 환경에서 그다지 좋지가 않다.
특히 false sharing이라는 문제가 발생하여 많은 프로세서가 있는 환경에서는 speedup이 좋지 않게 나온다. (False sharing을 좁은 공간에서 설명하기는 쉽지 않다. 그래도 최대한 간략하게 설명하면, 보통 캐쉬 라인의 크기는 64 바이트와 같이 여러 개의 데이터가 들어갈 수 있다. 그리고 여러 프로세서가 이 캐쉬 라인을 공유하면 이 단위로 공유가 된다. 그래서 같은 캐쉬 라인에 4바이트짜리 데이터가 두 개 있고 이 데이터가 각각 다른 CPU로부터 사용이 된다면, 불필요하게 이 캐쉬 라인을 invalidate시키는 문제가 발생한다(이 부분을 제대로 이해하려면 cache coherence protocol 중 대표적인 MESI 프로토콜을 알아야 한다). 생각보다 이 문제는 성능에 심각한 영향을 미친다.) 따라서 이러한 것도 고려하면 어떨까라는 답변을 하면 멋질 것이다. (멀티프로세서 환경을 고려한 대표적인 메모리 관리자로 Hoard memory allocator가 있다. http://www.hoard.org/를 방문해보라.)
[인터뷰 문제]
 이번에는 convex hull에 관한 문제이다. 그래픽스 수업을 듣지 않은 사람이라면 convex hull 자체에 대해서도 생소할 것이다. convex hull은 수학적인 의미도 있지만 좀 더 직관적으로 그림으
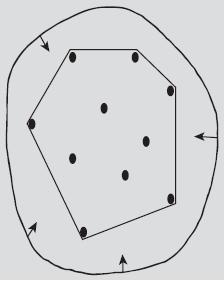
로 설명하면 주어진 점들을 감싸는 최소한의 공간을 뜻한다. 2차원 같은 경우는 아래 그림과 같다. (http://en.wikipedia.org/wiki/Convex_hull)
이번에는 convex hull에 관한 문제이다. 그래픽스 수업을 듣지 않은 사람이라면 convex hull 자체에 대해서도 생소할 것이다. convex hull은 수학적인 의미도 있지만 좀 더 직관적으로 그림으
로 설명하면 주어진 점들을 감싸는 최소한의 공간을 뜻한다. 2차원 같은 경우는 아래 그림과 같다. (http://en.wikipedia.org/wiki/Convex_hull)
그림에서 보다시피 오목한 부분 (concave)가 없고 볼록한 부분(convex)만 있다. 그렇다면 이 convex hull을 어떻게 하면 구할 수 있을까?
이 문제는 이미 오랫동안 연구된 것이고 좋은 time complexity를 가지는 알고리즘도 많이 발견되었다. 그러나 실제 면접 볼 때 이런 천재적인 알고리즘을 요구하는 것은 아니다. 가장 간단한 알고리즘부터 차근차근 만들고 좀 더 개선할 여지가 있는지를 생각해서 말하면 좋을 것이다. 여기서는 가장 간단한 방법만 하나 소개할 예정이다. 그리고 좀 더 자세한 내용은 흔히 CLRS 책으 로 불리는 유명한 알고리즘 책인『 Introduction to Algorithms』(B y Cormen, Thomas H., Leiserson, Charles E., Rivest, Ronald L., Stein, Clifford, MIT Press)를 참고하기 바란다.
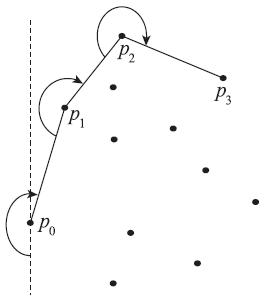
가장 간단한 방법 중 하나로 “Jarvis’s march(혹은 Gift wrapping)” 알고리즘이 있다. 말 그대로 감싸듯이 convex hull을 찾는 알고리즘이다. 아래 그림은 이 알고리즘이 어떻게 작동하는지 간단하게 보여주고 있다. (http://en.wikipedia.org/wiki/Gift_wrapping_algorithm)

먼저 가장 왼쪽에 있는 점인 P0를 찾는다. 그리고 다음 점 P1은 P0와 이루는 각이 가장 작은 녀석을 고르면 된다. 이 과정을 반복하면 convex hull을 찾을 수 있다. 앞서 소개한 CLRS 책에는 이와 다른 방법으로 알고리즘을 설명하고 있다. 다소 다르기는 하지만 전체적인 맥락은 차이가 없다. 다만 지금 그림에서 소개한 방법은 마지막으로 선택된 점의 각을 기억해야 한다. 그리고 하나 생각해볼 것은 가장 작은 각도를 만드는 점이 하나가 아니라 여러 개일 때 이것을 어떻게 해결할 것인가도 생각해보면 좋을 것이다. 이런 경우 영어로는 ~ breaks tie by selecting the furthest point ~와 같이 표현하면 된다.
이 알고리즘의 시간 복잡도를 계산해보자. 전체 점들의 개수를 n개라고 할 때, 다음 점을 찾는 과정은 각도를 구한 뒤 가장 작은 녀석을 찾으면 되므로 O(n)만큼의 시간이 걸릴 것이다. 그리고 이 과정을 convex hull에 포함될 점들의 개수 h만큼 수행하게 될 것이다. 따라서 알고리즘의 수행 시간은 O(nh) 꼴이 된다. 그래서 최악의 경우에는 h가 n과 같을 수가 있으므로 그 때는 O(n2) 알고리즘을 얻게 된다. 반면 h가 logn과 비슷하다면 이 방법은 상당히 우수한 성능을 보일 것이다. 그러나 알고리즘이 이렇게 미리 예측할 수 없는 h에 의존적이므로 항상 좋은 성능을 주는 것은 아니다. 반면 Graham’s Scan 방식은 O(nlogn)이라는 시간을 준다.
[인터뷰 문제]
주어진 두 정수를 나누는 함수를 만드는 문제이다. 물론 나눗셈 연산자(/)는 사용할 수 없다.
int my_divisor(int a, int b);
알고리즘은 간단하게 루프를 돌면서 a에서 b를 계속 빼면 몫을 구할 수 있다. 여기까지는 간단하나 여러 예외 사항을 잘 고려해야 한다. 일단 0으로 나눠지는 경우는 손쉽게 검사를 할 수 있다. 또한 주어진 수가 음수라면 절대값으로 만든 뒤에 계산을 하는 것이 편할 것이다. 그런데 단순히 절대값을 만들기 위해 -1을 곱하는 것은 문제가 발생할 수 있다. 보통 정수 표현은 2의 보수법(2’scomplement)으로 표현을 하는데, 음수의 범위가 양수보다 하나 더 크다. 예를 들어, 8비트라면 -128부터 127까지 표현이 가능하다. 따라서 -128에 단순히 -1을 곱하면 잘못된 값을 얻을 수 있다. 이 부분 역시 적절히 고려를 해야 할 것이다.
[인터뷰 문제]
문제는 간단하다. 예를 들어, {1, 7, 4, 9}라는 배열과 13이라는 숫자가 주어지면 4+9가 13을 만족하므로 답은 true가 될 것이다. 반면에 20이라는 숫자가 주어지면 만족하는 쌍이 없으므로 false를 반환하다. 혹은 하나 이상의 조합이 나올 수도 있는데, 이런 경우에는 어떤 것을 먼저 보여줘도 무방하다(이런 이야기를 해주지 않았으면 자기가 찾아서 이런 경우는 어떻게 하면 좋은지 직접 이야기를 하는 것이 좋다. 항상 면접 보는 사람과 많은 이야기를 하는 것이 중요하다).
가장 간단하게는 O(n2) 알고리즘으로 모든 쌍에 대해서 검사를 하는 것이다. 물론 이런 알고리즘을 요구하지 않는다. 이제 좀 더 좋은 성능을 위해 O(n) 만큼의 공간을 이용하는 방법을 생각해보자. 만약 hash table 자료 구조를 이용할 수 있다면 O(n) 시간에 답을 쉽게 구할 수 있다. hash table에 자료를 넣거나 검색하는 것은 상수 시간에 완료되기 때문이다. 그렇게 어렵지 않으므로 여기에 코드는 적지 않는다.
그러면 공간을 더 활용하지 않고 좀 더 똑똑히 할 수 있는 방법은 없을까? 만약 주어진 배열이 오름차순으로 정렬이 되어있다면? 이런 경우 공간은 더 사용하지 않으면서 O(n) 시간에 답을 구할 수 있는 방법이 있다.
먼저, 가장 작은 원소인 첫 번째 원소를 가리키는 왼쪽 인덱스 변수와 가장 큰 원소인 마지막 원소를 가리키는 오른쪽 인덱스 변수를 두자. 그리고 이 둘의 합을 구한 뒤 주어진 수와 크기를 비교하자. 만약 합이 주어진 수보다 작다면 왼쪽 인덱스를 증가시키고, 크다면 오른쪽 인덱스를 감소시킨다. 그리고 계속 반복을 하면서 같아지는지 확인을 하자. 루프는 최대 배열 원소의 개수만큼 반복하기 때문에 O(n) 시간에 완료된다. 코드는 아래와 같다.
bool FindSumOfPair(int A[], int N, int K)
{
int l = 0;
int r = N - 1;
int sum;
while (l < r)
{
sum = A[l] + A[r];
if (sum < K)
++l;
else if (sum > K)
--r;
else
return true;
}
return false;
}
만약 정렬이 comparison에 기초한 방법(Quicksort, Mergesort 등)이라면 최소 O(nlogn) 만큼의 시간이 걸릴 것이다. 결국 정렬 알고리즘이 시간 복잡도를 dominate하기 때문에 이 문제는 최고 O(nlogn) 시간에 해결할 수 있을 것이다. 반면 bucket sort처럼 O(n) 시간에 정렬을 할 수 있는 조건이라면 이 문제는 O(n)에도 풀 수 있다.
참고로 이 문제를 푸는 데 도움을 주신 iwongu, 시즈하, 에이쥬어, 그리고 silverbird님께 감사의 말씀을 전한다. 지금 생각하면 어렵지 않은 문제이다. 아니 쉬운 문제이다. 그런데 3시간 동안의 면접으로 지친 가운데 이런 문제를 또 받으면 머리가 아파서 더 생각하기가 귀찮을 정도였다. 사실 나는 hash table까지 이용하는 답이면 충분하다고 생각했는데, 난데 없이 추가 공간 없이 O(n)에 작동하는 걸 생각해보라는 질문을 듣고 당황하였다. 역시 면접 보기 전날 충분한 숙면과 컨디션 유지는 필요 조건임을 다시 깨달았다.
[인터뷰 문제]
n개의 비트로 이루어진 2진수에서 연속된 1이 나타나지 않는 경우는 몇 개나 있을까?
이 문제는 코딩 문제라기 보다는 퀴즈에 가까운 문제라고 볼 수 있다. 그러나 이 문제는 결코 간단하지 않는 귀납적 사고 능력을 요구하고 있다. 이런 귀납적 사고 능력은 실제 프로그래밍에서도(예를 들어, dynamic programming) 아주 유용하게 사용할 수 있는 것이므로 이러한 능력을 기르는 것은 매우 중요하다. 보통 이런 내용은 전산학과 과목 중 이산 수학에서 다룬다. 그리고 12장의 내용과도 어느 정도 방향을 같이 하는 것이라고 보면 될 것이다. 실제로 이런 문제를 인터뷰에서 묻는 경우도 있었다.
예를 가지고 문제를 다시 설명해보자. 2비트라면 총 가능한 경우의 수는 00, 01, 10, 11로서 4가지이다. 여기서 1이 연속으로 나타나지 않는 경우는 00, 01, 10 총 3가지이다. 이렇게 n개의 0과 1로 이루어진 수열에서 연속된 1이 없는 경우의 수(이것을 C(n)으로 표현하자)를 찾는 것이 이 문제가 요구하는 답이다. 이런 문제의 시작은 일단 손으로 낙서를 해가며 규칙을 찾아야 한다. C(3)까지 한 번 직접 구해보자.
C(1) = {0, 1}: 2개
C(2) = {00, 01, 10}: 3개
C(3) = {000, 001, 010, 100, 101}: 5개
수학과 조금 친한 사람이라면 대략 여기서 바로 피보나치 수열임을 짐작하고 C(4)을 손으로 구해 확인한 후 정답으로 바로 말할 수 있을 것이다. 그러나 이런 직관적인 방법 말고 좀 더 수학적인 방법으로 답을 유도해보자.
이런 순열의 경우 일반항을 구하기 위해서는 점화식을 찾는 것이 첫번째로 할 일이다. 점화식은 영어로 recurrence로 표현이 되며, 각종 재귀 알고리즘의 시간 복잡도를 기술하는 데도 많이 사용된다. 예를 들어, merge sort의 경우 T(n) = 2T(n/2) + O(n)으로 표현되고 Master"s theorem을 통해 O(nlogn)을 얻을 수 있다(자세한 것은 이산수학 책과 알고리즘 책을 참고하기 바란다).
점화식을 찾기 위해 수학 시간에 배운 수학적 귀납법을 이용해보자. C(n)의 해를 가지고 있다고 가정하자. 그리고 이제 C(n+1)을 기존의 해인 C(n)로 표현해보자.
숫자가 하나 더 늘었다는 소리는 n개의 순열 앞에 0 또는 1을 더 붙이는 것과 같다. 먼저 0이 추가되는 경우를 생각해보자. 생각하기 쉽게 이미 구한 C(3)을 가지고 생각하자. 이미 구한 5개의 답에 0을 앞에다 붙여도 여전히 이들은 주어진 조건을 만족하며 답으로 남는다. 즉, C(3)의 해를 고스란히 가져올 수 있다. C(4)에는 {0000, 0001, 0010, 0100, 0101}이 해로 포함이 될 것이다.
이제 1이 추가되는 경우를 생각해보자. 마찬가지로 C(3)의 해에다가 1을 더해보자. 앞의 3가지인 000, 001, 010은 문제 없다. 그러나 마지막 두 개는 1이 앞에 올 경우 1100처럼 되기 때문에 조건에 위배된다. 여기서 약간의 눈썰미를 동원해보자. 1을 더해도 조건을 만족하는 수들은 1000, 1001, 1010의 3가지이다. 그런데 이들은 처음 시작이 10으로 시작함을 알 수 있다. 그리고 그 뒤에 붙는 00, 01, 10은 C(2)의 해와 정확히 일치함을 발견할 수 있다. 즉, C(2)의 해에다가 10을 덧붙이는 것도 C(4)의 해가 된다.
따라서 C(4)는 결국 C(3)에다 0을 덧붙인 경우와 C(2)와 01을 덧붙인 경우로 생각할 수 있다. 즉, C(n)은 C(n-1) + C(n-2)가 되는 것이다. 그리고 이것은 바로 피보나치 수열과 정확하게 일치한다. 따라서 최종 정답은 아래와 같다.
C(n) = C(n-1) + C(n-2) (단, n은 n>2인 정수, C(1) = 2, C(2) = 3)이 문제를 다시 살펴보면, C(n)을 풀기 위해 이미 풀어놓은 해들을 잘 활용했음을 볼 수 있다. 이것은 동적 프로그래밍의 접근 방식과 동일하다. 동적 프로그래밍 방법론의 일반적인 접근 방식은 다음과 같다.
먼저 문제 중 겹치는 부분이 있는가를 찾아야 한다. 풀이에서도 이미 보았듯이 C(n+1)의 해에는 C(n)의 해가 겹쳐있다. 이 관계를 잘 분석해서 점화식으로 표현을 한다. 그리고 bottom-up으로 값들을 차례대로 계산하면 원하는 답을 얻을 수 있다. 대표적으로 matrix-chain multiplication, longest common subsequence와 같은 문제가 있다. 단순히 리스트, 트리와 같은 자료 구조에 관련된 공부뿐만 아니라 동적 프로그래밍 혹은 greedy algorithm과 같이 알고 리즘 방법론도 숙지해야 할 것이다. 앞의 convex hull 문제에서 소개한 CLRS 책에는 이런 방법론들이 아주 자세히 설명되어 있다.
자, 그러면 응용 문제를 하나 더 풀어보자. 주어진 문제는 “연속된 1이 나타나지 않는 경우의 수”였다. 그러면 이 반대인 “연속된 1이 나타나는 경우의 수”는 어떻게 될까? D(n)을 구하고자 하는 수라고 표현하면 다음과 같을 것이다:
D(1) = {ø}: 0개
D(2) = {11}: 1개
D(3) = {011, 110, 111}: 3개
D(4) = {0111, 0110, 0111, 1011, 1100, 1101, 1110, 1111}: 8개
여기서 한 번 D(n)의 점화식을 구해보자. C(n)을 구하는 것보다는 약간 어렵다. 그러나 앞의 문제 풀이를 제대로 습득하였다면, 큰 어려움 없이 풀 수 있으리라 생각된다. 정답은 맨 마지막을 참고하기 바란다.
[인터뷰 문제]
어떤 숫자가 2의 거듭제곱수 (2, 4, 8, 16, 32, 64 , ...)인지 아닌지를 판단하는 코드를 작성하시오.
지금 소개한 문제는 정식 인터뷰에서 받은 문제가 아니라 Job Fair 같은 곳에서 이루어진 일종의 쪽지 시험에서 나온 문제였다. 앞에서도 이미 아마존 같은 기업은 이력서를 받는 그 자리에서 C 키워드 중 volatile이 무엇을 하는지 묻기도 한다고 쓴 바가 있다. 이 문제는 실제 Job Fair에서 어떤 기업이 이력서를 받으면서 학생들에게 준 간단한 코딩 테스트이다 그러나 결코 만만치 않은 문제일 수 있다.
만약 숫자들이 컴퓨터로 어떻게 표현이 되는지에 대한 정보가 없다면 다소 까다롭고 복잡한 루틴이 나올 수 있다(예를 들어, 2로 나눈 뒤에 나머지가 있는지 확인하고, 이 과정을 몫이 1이 될 때까지 반복하면 될 것이다). 그러나 거의 모든 컴퓨터들은 정수 표현을 2의 보수로 하기 때문에 이 특징을 활용하면 훨씬 빨리 문제를 풀 수 있다. 따라서 이 문제를 풀기 전, 문제에서 주어진 숫자들은 부호와 2의 보수로 주어졌다고 가정을 해보자. 항상 문제를 풀 때 부족하다고 느껴지는 가정은 쓰는 것이 좋다. 그리고 이 가정을 세우는 것도 중요한 능력 중에 하나이다.
먼저 2의 거듭제곱수들을 2진수로 표현을 해보자. 금방 규칙 하나를 발견할 수 있을 것이다. 오직 한 자리수만 1로 되어있고 나머지는 모두 0임을 확인할 수 있다. 단순하게는 32 혹은 64번만큼 루프를 돌면서 1이 하나만 켜져 있는지 보면 될 것이다. 아니면 대부분의 CPU가 지원하는 기본 명령인 BitScanForward와 BitScanReverse를 이용하는 방법도 있을 것이다. 14 LSB에서 시작하여 MSB로 가면서 1이 발견되면 그 위치를 알려주는 함수들이다(Reverse는 MSB에서 LSB로 탐색). 그래서 이 두 함수로부터 얻은 위치가 같으면 2의 거듭제곱수라고 판단할 수 있다. 그러나 이렇게 해도 뭔가 깔끔하고 아름답지가 못하다. 더 좋은 방법이 있다.
주어진 숫자에서 1을 한 번 빼보자. 그러면 2진수 표현 방법으로는 가장 먼저 발견된 1 뒤의 모든 숫자들이 모두 1로 변할 것이다. 그리고 원래 수와 AND연산을 한다면? 2의 거듭제곱수라면 결국 0이 얻어질 것이다. 이것이 가장 빠른 2의 거듭제곱수 판단 방법이다. 예를 들면 다음과 같다. x는 2의 거듭제곱수이고, y는 그렇지 않은 수이다.

이 정도면 충분히 이 원리에 대해서 이해가 갔으리라 믿는다. 그러나 여기서도 또 예외가 하나 있다. Boundary check를 해야 하는데, 0이 주어진다면 이 테스트로는 참이 얻어질 것이다. 또, 음수도 무시해야 할 것이다. 따라서 최종 정답은 (x > 0) && ((x & (x - 1)) == 0) 이 될 것이다. 좀 더 엄밀하게 말해 이 조건은 부호와 2의 보수로 표현된 정수 x가 2의 거듭제곱수인가와 필요충분조건을 이룬다.
[인터뷰 문제]
다음 매크로가 하는 일이 무엇인지 기술하시오.
#define foo(a, b) ( (size_t) &((a)NULL)->b )
많은 프로그래밍 경험이 있다면 이 매크로가 무엇을 하는 것인지 금방 알아차릴 것이지만, 그렇지 않다면 당혹스러울 수 있다. NULL을 이상하게 캐스팅을 하고 거기에 멤버 변수까지 접근하니 “이거 버그 아니야?”라고 갸우뚱할 수 있다. 그러나 이것은 올바른 코드이고 자주 사용되는 매크로이다.
이것은 주어진 class 혹은 struct에서 특정 멤버 변수의 offset을 알아내는 것이다. 컴파일러마다 혹은 컴파일러 옵션마다 struct 자료 구조에서 멤버 변수들의 공간을 할당할 때, alignment가 다를 수가 있다. 그래서 클래스에서 어떤 멤버 변수가 얼마나 떨어져 있는가를 알고 싶다면 이 매크로를 사용하여 유용하게 알 수 있다. 이 매크로의 경우에 a에는 클래스에 대한 포인터, b에는 멤버 변수 이름을 넘겨주면 이 변수의 오프셋을 알 수 있다. 0번 주소라는 잘못된 주소를 강제로 주어진 클래스 포인터 타입으로 바꾼 뒤에 멤버 변수의 주소를 반환하는 것이다.
예제 코드를 통해 이 매크로가 어떻게 작동하는지 살펴보자.
struct Rectangle
{
int top;
int left;
int bottom;
int right;
};
#define foo(a, b) ( (size_t) &((a)NULL)->b )
int offset = foo(struct Rectangle*, bottom);
위와 같은 코드를 컴파일하면 일반적인 경우 offset에 8이라는 숫자가 얻어짐을 확인할 수 있다(물론, 컴파일러마다 컴파일러 세팅 마다 값이 다를 수 있다).
이런 매크로를 이용한 장난은 상당히 다양한데, 그래도 C/C++을 자신있게 다룬다고 말을 할 수 있다면 간단한 매크로 구문은 충분히 숙지해야 할 것이다.대표적으로 #define에서 사용되는 #와 ## preprocessor operator들이 있다. #는 stringizing operator라고 불리며 주어진 내용을 따옴표로 감싸 문자열로 바꿔주는 역할을 한다. ##는 Token-Pasting 혹은 merging operator라고 불 리며 앞 토큰과 뒤에 있는 토큰15을 이어주는 역할을 한다. 좀 더 자세한 예는 검색을 통해서 쉽게 찾을 수 있을 것이다.
지금까지 8문제를 풀어보았다. 보다시피 그 자리에서 아주 높은 수준의 번뜩이는 천재성을 요구하는 문제는 없다. 모두 기본적인 전산 실력이 있으면 풀수 있는 내용들이다.
마지막으로 이 문제들 외에 실제 면접에서 받은 문제 몇 개를 간략하게 소개하면 다음과 같다.
- 숫자를 문자열로 바꾸는 문제(혹은 그 반대, 유니코드 관련 문제도 언급하 면 좋을 것이다)
- 그래프 알고리즘 중 DFS/BFS를 응용하는 문제(반드시 이 두 가지 순회 방 법은 숙지하길 바란다)
- MODE(주어진 샘플에서 가장 많은 빈도로 나타나는 값)을 찾는 알고리즘
- Linked List를 가지고 뒤집는 등의 연산을 하도록 하는 함수 만들기
- Quicksort 알고리즘 중 partition 알고리즘을 응용한 문제
[정답]
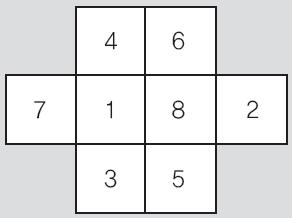
- 8개의 박스에 숫자 채워 넣기 퍼즐의 정답은 아래와 같다.
- 경우의 수에 대한 답은 8!/(3!*5!)=56 가지이다.
- D(n)의 점화식은 다음과 같다.
D(n) = D(n-1) + D(n-2) + 2n-2, (단, n은 2보다 큰 정수이며, D(1) = 0, D(2) = 1)
TAG :
이전 글 : 마이크로소프트 인턴 면접기(2)
다음 글 : C로 개발하면 안되나요? (1)
최신 콘텐츠